Problem: storing passwords is hard
You're a system administrator and -- oh no! A hacker stole your database!
Well, not yet... but they could. Once you get popular enough it's bound to happen.1 Can you make sure your users data is safe when that happens?
When you store passwords in a database you never store them in plain text. Instead, you store a hash of that password. For example:
Password: 12345678
sha256sum (hash): 2634c3097f98e36865f0c572009c4ffd73316bc8b88ccfe8d196af35f46e2394
The hash is generated when the user tries to login. The hash of the password the user sends at login is compared against the corresponding password hash for that user. If it matches that means the user sent the right password and so they are authenticated.
What happens if the hacker pre-computes a bunch of popular passwords?
This might sound crazy, but there are lots of people that re-use passwords, like 123456.
The hacker can pre-compute the hash for the 1,000,000 most popular passwords and more or less reverse-search for any user's password once they have a database dump.
Solution 1: add salt
Our first naive solution to solve this problem is to make the adversary's life harder by adding salt to our passwords. This is a piece of known information which is added to the password so adversaries can't pre-compute a hash-table, they have to compute this after they have the database and figure out the salt. For example:
Password: 12345678
Salt: cryptoHeckYeah!
New Password: 12345678cryptoHeckYeah!
sha256sum: 6e8a7780df48a0b687e9e272e8d082f5f4c0c3a8c43b63461c3f62618b111e9d
Unfortunately we live in 2017 and Graphics processors and ASICs are cheap and can compute sha256sums super fast for really cheap. This means that it might be more of a pain, but the adversary can still crack a password with relative ease and efficiency because they've got a computer designed to generate lots of hashes. Curses.
Solution 2: H(H(..H(x)..)
Computing a single sha256sum is easy, but what if the hacker had to compute like... 1000 sha256sums for each password! That sounds pretty hard... right? If we compute the hash of the hash of the hash (etc) it would take like... 1000x longer to compute each user's password. Something like this:
p = '12345678cryptoHeckYeah!'
for x in 1..1000
p = sha256sum( p )
end
return p
Result: 47c76630def739ede9c05fd974065b1200d4712aa2421eefb1f6b241a1ca6bea
Time: 0m1.547s
Unfortunately this hurts more than it helps.
In bash on non-specialized hardware, this took about 1.6 seconds. On specialized hardware, written in a systems programming language, and implemented in parallel it'd be much less costly for an adversary to crack passwords hashed this way.
Worst of all, this is easier for an adversary to compute than it is for the the "good guys" because the non-malicious actor is using generalized hardware and the adversary is using specialized hardware to compute the hashes. It's like trying to beat a Roadster in a drag race when you're behind the wheel of a Minivan; the Minivan ("good guys") can't win because they weren't built for drag races.
Solution 3: Memory Hard Functions
The big problem we have is that CPUs can be specialized to crack passwords very quickly. No matter how fast your AWS EC2 instance is, or even that top of the line IBM server you just bought, it will never be faster than a cheap custom designed ASIC. At around 3000$/box it won't break the adversary's bank to break into yours.2
While there specialized hash-cracking CPUs do exist, specialized hash-cracking memory does not exist.3 If we were to create an algorithm which depends on lots of memory, instead of lots of CPU cycles, we could "level the playing field". This should help stop adversaries from reversing passwords as fast as they currently can.
This theoretical hash-function is called a Memory Hard Function (MHF). These are difficult to perform unless you have a certain threshold of memory. As a result non-malicious actors can perform a hash in M seconds and it will take a malicious actor at least M seconds to perform the same hash.
Note <p>TLDR: We want a hash function that takes as long for an adversary to compute as it does for the "good guys" to compute. Since nobody has specialized hash-cracking RAM we should be able to create a hash function which is memory-intensive and fits our criteria. If we have a function that fits this we will have got a <em>Memory hard Function</em> (MHF).</p>scrypt: a wild MHF
scrpyt is a key derivation function developed for the Tarsnap project. It was designed explicitly to solve this problem and has some pretty impressive results. Some especially impressive results include:
- scrypt is about 25 times more expensive to attack for logins than bcrypt.
- scrypt is about 215 times more espensive to attack for logins than MD5 CRYPT.
- scrypt is about 237 times more expensive to attack for file encryption than MD5.
scrypt also happens to be a MHF. Yay we found one!
So... how does it work?
Given a hash function H, an input B, and an integer N, compute:
Vi = Hi(B), given 0 ≤ i < N,
and
X = HN(B)
then iterate
- j <- Integrify(X) mod N
- X <- H(X ⊕ Vj)
N times; and output X
The function Integrify can be any bijection4 from {0,1}k to {0...2k - 1}.
Breaking that down a bit:
- The function is given a different hash function (H), an input to compute the hash of (B), and a modulus (N).
- N hashes are generated with variations of H and the input B called V0..N.
- X is initialized with a hash value and a loop begins:
- j is set to a psuedo-random integer mod N.
- X is set to the hash of the existing X value xor'd with one of the V values.
- Loop N times and output the final X.
One of the biggest gripes with scrypt is that it has a very predictable runtime. This means that the running of the function is predictable based on the user's input and so can be victim to a cache-timing side-channel attack. We won't be able to get into what this attack means, but basically you can say "scrypt is good, but not perfect".
Data-independent MHFs (iMHFs)
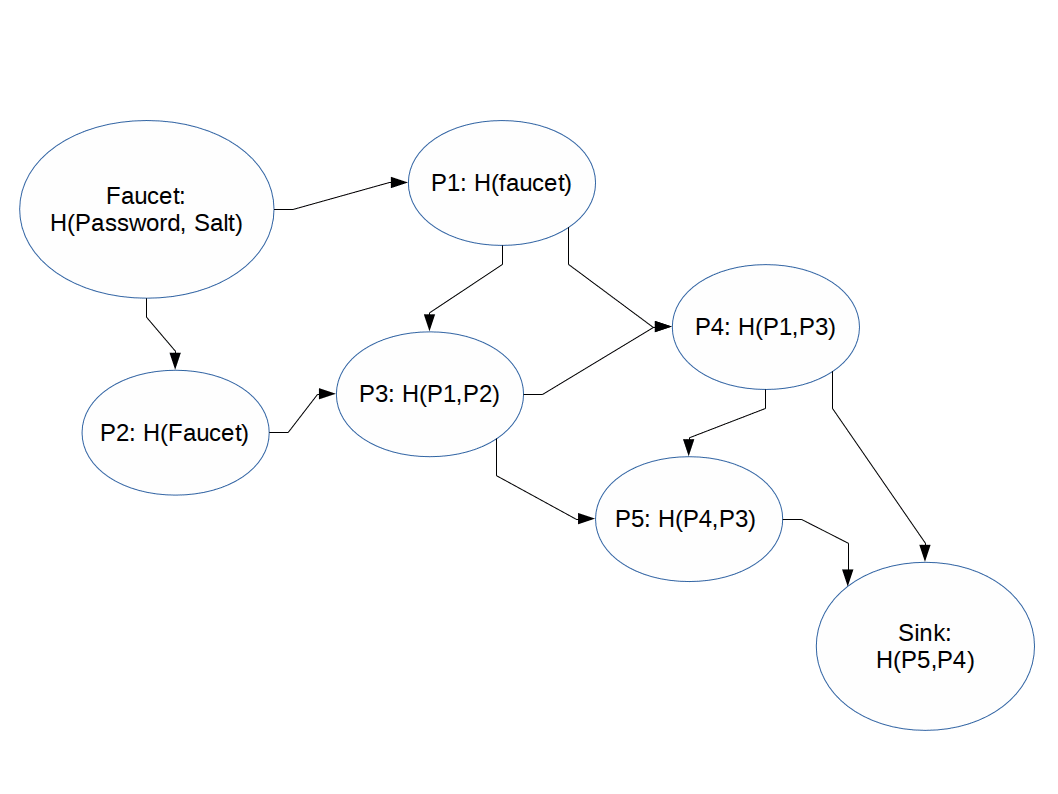
iMHFs are supposed to solve the problem that scrypt has (side-channel attacks) by have unpredictable runtimes which still result in the same output.
iMHFs can be thought of as Directed Acyclic Graphs (DAGs) which are traversed during runtime.
Some specifics:
- The function depends on a random oracle H: {0,1}2k -> {0,1}k
- The function provides a Directed Acyclic Graph Directed Acyclic Graph (DAG) G used to encode data-dependencies
- The initial input is a password and a salt.
- Each other node is labeled with the hash of it's parent nodes.
- The output is the hash of the value of the last node.
As mentioned before, a very nice feature of iMHFs is that their memory usage pattern does not depend on the user's input (password) and so is not vulnerable to side-channel attacks.
Pebbling a Directed Acyclic Graph (DAG)
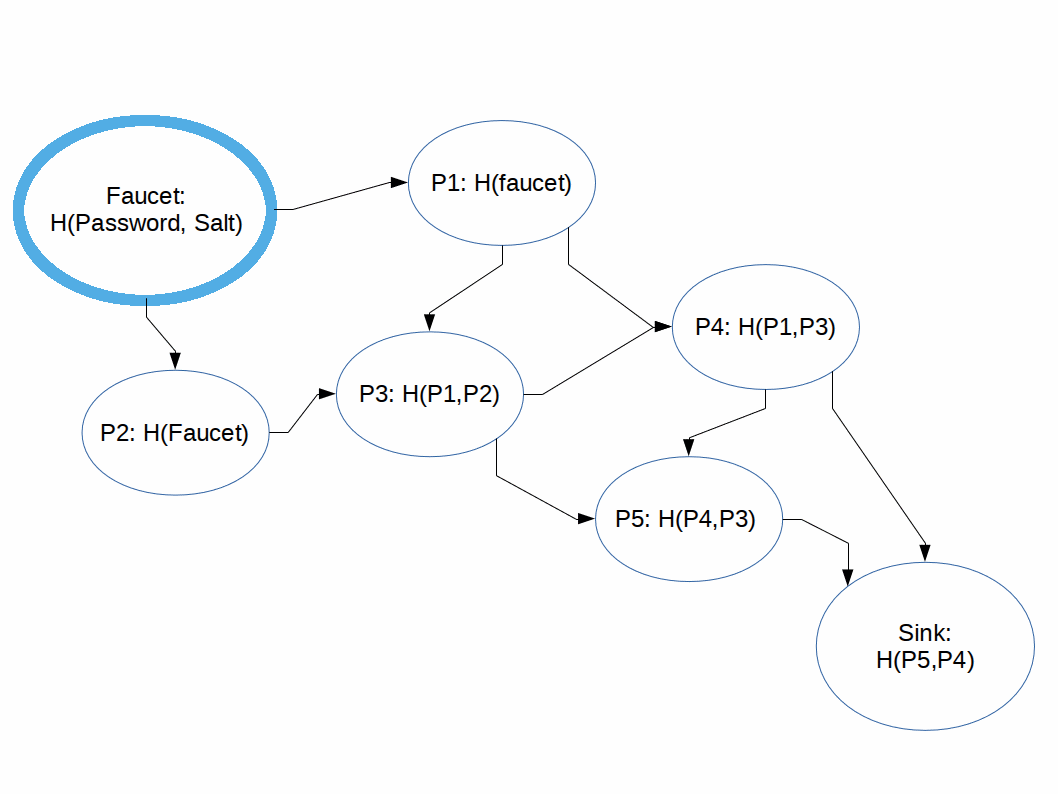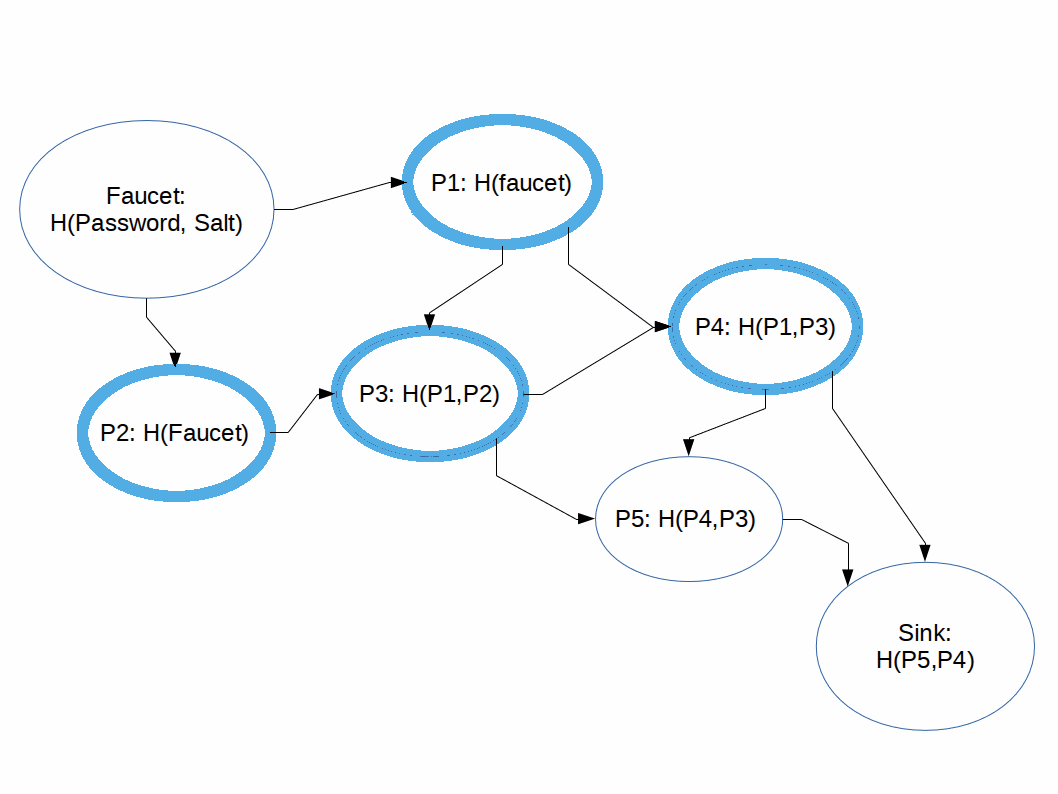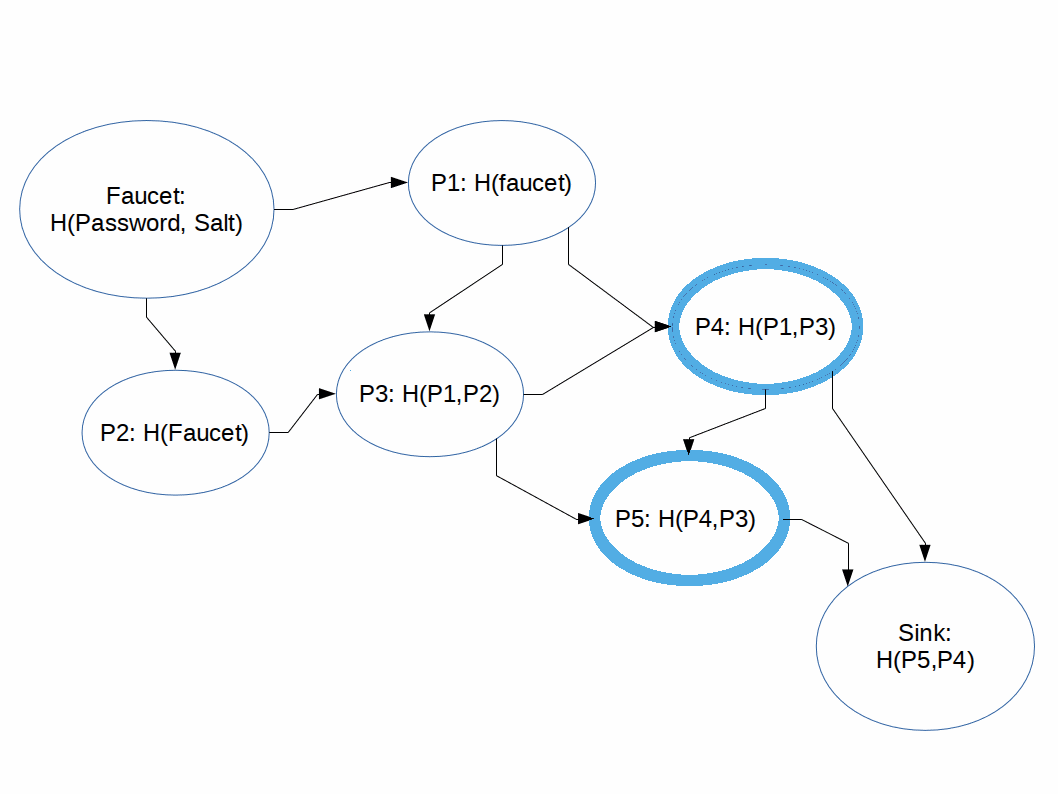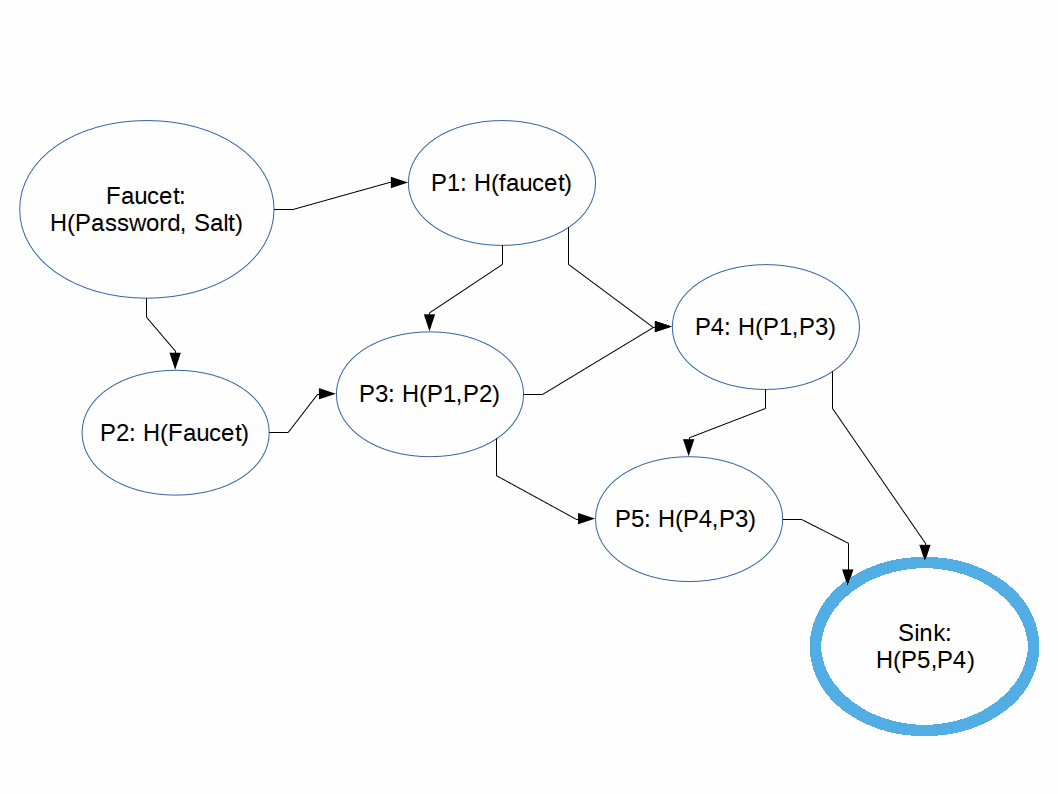
We can think of the process of computing the output of an iMHF as pebbling a graph where:
- Computing the value of a node is to pebble it.
- There are rules about which nodes can be pebbled at any time.
- When a pebble is removed from a node it is freed from memory.
- Our goal is to pebble the last node.
Rules:
- We can only place a pebble on a node if we have pebbles on all of it's parents nodes.
- Our goal is to get to the sink node (exit node).
The naive pebbling algorithm, the one the 'good guy' user would utilize is as follows:
- Only one pebble can be placed per time-step.
- The graph is pebbled in in topological order.
- Pebbles (calculated nodes) are never discarded until the end of the function.
- Expected cost: scales with n2 where n is the number of nodes.
This does take up considerable resources, but it isn't prohibitive for users on commodity hardware. This means it won't take too long to get your account authenticated. More importantly, it will take about as long for the bad guys to calculate a token as it took you to calculate a token, as opposed to a small fraction it would take if this was a "normal" hash function.
Attacks on iMHFs
An attack is defined as when cost of calculating a hash from an iMHF is lower than via the nieve approach.
The general idea of an iMHF attack is that it has two phases: light phase and balloon phase.
Light Phase
In the light phase the algorithm races through the DAG discarding as many pebbles as possible, essentially performing a breadth first search for the end of the graph, computing nodes in parallel when possible. Once a node is computed and it isn't immediately needed it is discarded.
If the DAG were a straight line from beginning to end this would be fairly memory efficient.
Balloon Phase
In the balloon phase the algorithm has 'hit a wall' and back-computes the nodes it needs to compute the next node whose parent's have already been discarded. This causes a slow-down.
An attack described like this has the following complexity:
ER(A) = O(en + √(n3d))
For small values of e and d this results in an attack as:
ER(A) = O(n2) for e,d = O(n)
Preventing against this type of attack is where much of the research into iMHF's is focused. An ideal iMHF DAG minimize the disparity between the attackers compute time and the "good guy's" compute time.
Conclusion
This has been a rough overview of Memory Hard functions, how they work, and how variations of MHFs differ.
MHFs are functions which remove the advantage that adversaries have to crack passwords by depending heavily on memory. This reduces the adversary's advantage if they have an ASIC or GPU processor(s) to brute-force a password crack and ought to make it very difficult (ideally impractical) for adversaries to crack a password hashed with an MHF.
Some existing MHFs, like scrypt, are vulnerable to side-channel attacks so iMHFs have been theorized which do not have a predictable runtime and so are not vulnerable to side-channel attacks. No iMHFs exist yet, however many functions have been developed with get close and offer many of the benefits of iMFHs. Some of these include Argon2i, Catena, and Balloon hashing, which we did not cover in this post.
Annotated Bibliography
Conference Presentations by Jeremiah Blocki[^5][^6]5 The video presentations online by Jeremiah were a very important resource for getting a grasp on what MHFs are, and more specifically what iMHFS and how they worked. The three videos cited in this post cover largely the same content and present the material, including the problem, naive solution, MHF solution, iMFH solution, and possible attacks against iMHFs in about 30 minutes. I like to think I'm pretty good at public speaking, but this material was very complicated and presented in a very digestible format.
I cannot stress enough how useful these videos were. I learned an incredible amount from these videos and referenced them for the majority of this content.
Strict Memory Hard Hashing Functions6 This paper was very short and presented some essential knowledge to discuss the differences between MHFs and iMHFs. I didn't directly use or reference this content, however it did present an easily understandable academic definition and comparison of iMHF compared to MHFs.
Practical Graphs for Optimal Side-Channel Resistant Memory-Hard Functions7 This paper was used in the writing of this post, however it was very long and dense, so it was never directly cited.
scrypt: A new key derivation function8 This was the soul reference for the scrypt section of this post. There is an academic paper published too, but the slides were simple and presented all of the same knowledge (I think) sans any proofs.
If I feel an existential hole in my heart I might read the proofs, but in the interest of time I chose not to right now.
Errata
Antminer "Bitcoin Miner" http://a.co/2E20HW8
Yet.
Bijection: A function which creates a 1-to-1 relationship between inputs and outputs.
Efficiently Computing Data Independent Memory Hard Functions (Video) Joël Alwen and Jeremiah Blocki, Crypto 2016, September 26, 2016, https://youtu.be/ujpvPtn_N5Y
Towards a Theory of Data-Independent Memory Hard Functions (Video), Jeremiah Blocki with Joel Alwen, Krzysztof Pietrzak 2017, Real World Crypto conference, February 1, 2017, https://youtu.be/YtfVLzUkwME
Memory Hard Functions and Password Hashings (Video), CERIAS Symposium 2017 - TechTalk, Jeremiah M. Blocki - Assistant Professor, Computer Science - Purdue University, May 1, 2017, https://youtu.be/9yX4v89m5oo
Strict Memory Hard Hashing Functions, Sergio Demian Lerner, (Preliminary v0.3, 01-19-14), http://www.hashcash.org/papers/memohash.pdf
Practical Graphs for Optimal Side-Channel Resistant Memory-Hard Functions Joel Alwen, Jeremiah Blocki, Ben Harsha IACR Cryptography ePrint Archive, 2017, https://eprint.iacr.org/2017/443.pdf
scrypt: A new key derivation function (variable subtitles) Colin Percival, May 9, 2009, http://www.tarsnap.com/scrypt/scrypt-slides.pdf